NIPS 2021, top-5 papers:
1.Deep Networks Provably Classify Data on Curves
Our analysis proceeds by a reduction to dynamics in the neural tangent kernel (NTK) regime, where the network depth plays the role of a fitting resource in solving the classification problem. In particular, via fine-grained control of the decay properties of the NTK, we demonstrate that when the network is sufficiently deep, the NTK can be locally approximated by a translationally invariant operator on the manifolds and stably inverted over smooth functions, which guarantees convergence and generalization.
2.Low-Rank Subspaces in GANs
By contrast, this work introduces low-rank subspaces that enable more precise control of GAN generation. Concretely, given an arbitrary image and a region of interest (e.g., eyes of face images), we manage to relate the latent space to the image region with the Jacobian matrix and then use low-rank factorization to discover steerable latent subspaces. There are three distinguishable strengths of our approach that can be aptly called LowRankGAN. First, compared to analytic algorithms in prior work, our low-rank factorization of Jacobians is able to find the low-dimensional representation of attribute manifold, making image editing more precise and controllable. Second, low-rank factorization naturally yields a null space of attributes such that moving the latent code within it only affects the outer region of interest. Therefore, local image editing can be simply achieved by projecting an attribute vector into the null space without relying on a spatial mask as existing methods do. Third, our method can robustly work with a local region from one image for analysis yet well generalize to other images, making it much easy to use in practice.
3. Rethinking conditional GAN training An approach using geometrically structured latent manifolds
we tackle this problem from a geometrical perspective and propose a novel training mechanism that increases both the diversity and the visual quality of a vanilla cGAN, by systematically encouraging a bi-lipschitz mapping between the latent and the output manifolds. We validate the efficacy of our solution on a baseline cGAN (i.e., Pix2Pix) which lacks diversity, and show that by only modifying its training mechanism (i.e., with our proposed Pix2Pix-Geo), one can achieve more diverse and realistic outputs on a broad set of image-to-image translation tasks
4.Towards Lower Bounds on the Depth of ReLU Neural Networks
We contribute to a better understanding of the class of functions that is represented by a neural network with ReLU activations and a given architecture. Using techniques from mixed-integer optimization, polyhedral theory, and tropical geometry, we provide a mathematical counterbalance to the universal approximation theorems which suggest that a single hidden layer is sufficient for learning tasks
5. Intrinsic Dimension, Persistent Homology and Generalization in Neural Networks
By making a novel connection between learning theory and TDA, we first illustrate that the generalization error can be equivalently bounded in terms of a notion called the ’persistent homology dimension’ (PHD), where, compared with prior work, our approach does not require any additional geometrical or statistical assumptions on the training dynamics. Then, by utilizing recently established theoretical results and TDA tools, we develop an efficient algorithm to estimate PHD in the scale of modern deep neural networks and further provide visualization tools to help understand generalization in deep learning
1.Deep Networks Provably Classify Data on Curves
Our analysis proceeds by a reduction to dynamics in the neural tangent kernel (NTK) regime, where the network depth plays the role of a fitting resource in solving the classification problem. In particular, via fine-grained control of the decay properties of the NTK, we demonstrate that when the network is sufficiently deep, the NTK can be locally approximated by a translationally invariant operator on the manifolds and stably inverted over smooth functions, which guarantees convergence and generalization.
2.Low-Rank Subspaces in GANs
By contrast, this work introduces low-rank subspaces that enable more precise control of GAN generation. Concretely, given an arbitrary image and a region of interest (e.g., eyes of face images), we manage to relate the latent space to the image region with the Jacobian matrix and then use low-rank factorization to discover steerable latent subspaces. There are three distinguishable strengths of our approach that can be aptly called LowRankGAN. First, compared to analytic algorithms in prior work, our low-rank factorization of Jacobians is able to find the low-dimensional representation of attribute manifold, making image editing more precise and controllable. Second, low-rank factorization naturally yields a null space of attributes such that moving the latent code within it only affects the outer region of interest. Therefore, local image editing can be simply achieved by projecting an attribute vector into the null space without relying on a spatial mask as existing methods do. Third, our method can robustly work with a local region from one image for analysis yet well generalize to other images, making it much easy to use in practice.
3. Rethinking conditional GAN training An approach using geometrically structured latent manifolds
we tackle this problem from a geometrical perspective and propose a novel training mechanism that increases both the diversity and the visual quality of a vanilla cGAN, by systematically encouraging a bi-lipschitz mapping between the latent and the output manifolds. We validate the efficacy of our solution on a baseline cGAN (i.e., Pix2Pix) which lacks diversity, and show that by only modifying its training mechanism (i.e., with our proposed Pix2Pix-Geo), one can achieve more diverse and realistic outputs on a broad set of image-to-image translation tasks
4.Towards Lower Bounds on the Depth of ReLU Neural Networks
We contribute to a better understanding of the class of functions that is represented by a neural network with ReLU activations and a given architecture. Using techniques from mixed-integer optimization, polyhedral theory, and tropical geometry, we provide a mathematical counterbalance to the universal approximation theorems which suggest that a single hidden layer is sufficient for learning tasks
5. Intrinsic Dimension, Persistent Homology and Generalization in Neural Networks
By making a novel connection between learning theory and TDA, we first illustrate that the generalization error can be equivalently bounded in terms of a notion called the ’persistent homology dimension’ (PHD), where, compared with prior work, our approach does not require any additional geometrical or statistical assumptions on the training dynamics. Then, by utilizing recently established theoretical results and TDA tools, we develop an efficient algorithm to estimate PHD in the scale of modern deep neural networks and further provide visualization tools to help understand generalization in deep learning
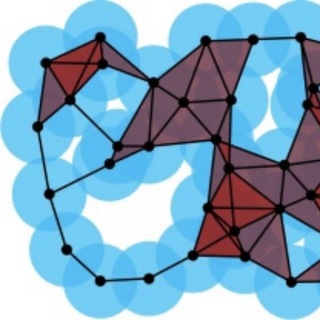
Low-dimensional structure in image data and the two curves problem. Left: Manifold structure in natural images arises due to invariance of the label to continuous domain transformations such as translations and rotations. Right: The two curve problem. We train a neural network to classify points sampled from a density ρ on the submanifolds M+,M− of the unit sphere. We illustrate the angle injectivity radius ∆ and curvature 1/κ. These parameters help to control the difficulty of the problem: problems with smaller separation and larger curvature are more readily separated with deeper networks
(from Deep Networks Provably Classify Data on Curves)
(from Deep Networks Provably Classify Data on Curves)
Forwarded from gonzo-обзоры ML статей
[ConvNeXt] A ConvNet for the 2020s
Zhuang Liu, Hanzi Mao, Chao-Yuan Wu, Christoph Feichtenhofer, Trevor Darrell, Saining Xie
Статья: https://arxiv.org/abs/2201.03545
Код: https://github.com/facebookresearch/ConvNeXt (нормально так, что у несколькодневной репы уже 1.7К звёзд)
Империя наносит алаверды.
После всех этих историй с заменой свёрточных сетей на трансформеры (ViT, https://www.tgoop.com/gonzo_ML/434), а затем на старые добрые полносвязные сети (https://www.tgoop.com/gonzo_ML/800), явно должно было быть что-то ответное от свёрточных сетей в духе, что вы их готовить не умеете. И вот, пожалуйста :)
Свежая работа от 10 января 2022 из главного центра экспертизы по свёрточным сетям им. Яна Лекуна (FAIR) + Беркли.
Это снова история и про то, нужны все эти inductive biases или нет, в них соль или нет. Польза от inductive biases свёрточных сетей, особенно translation equivariance, очевидно, есть, раз значительная доля продвинутых модификаций трансформеров и MLP ушла в сторону гибридизации и привнесения свойств свёрток в эти модели. А если так, то может достаточно и свёрточных моделей, раз в них уже всё нужное есть?
Авторы поступили просто — взяли стандартный ResNet и постепенно прошли путь, добавляя в него разные вещи, показавшие себя хорошо в трансформерах (сохраняя при этом количество вычислений на примерно одинаковом уровне, чтобы было честно). И добились таки чисто свёрточной архитектуры (ConvNeXt), бьющей лучшие имеющиеся трансформеры аналогичных размеров (имеется в виду Swin Transformer, https://github.com/microsoft/Swin-Transformer).
В качестве объектов берут сети двух размеров ResNet-50/Swin-T и ResNet-200/Swin-B, также оценивают скейлинг на модели размера XL, но дальше не идут, так что сравниться напрямую со Swin V2 (https://arxiv.org/abs/2111.09883) размеров H и G не получится.
Во-первых, начальные резнеты обучают аналогичными ViT процедурами, и это само по себе уже даёт повышение качества (Top-1 accuracy на ImageNet) с 76.1% до 78.8% для ResNet-50. Сюда входит много всяких изменений и улучшений: 300 эпох вместо 90, оптимизатор AdamW, аугментации через Mixup, Cutmix, RandAugment, Random Erasing, регуляризации включая stochastic depth и label smoothing. Если вы с чем-то из этого ещё не знакомы и всё ещё кипятите, то это хороший повод набраться актуальных рецептов. В статье все ссылки есть.
Дальше изменения бьются на несколько блоков.
1. Макро дизайн.
Тут изменяют соотношение compute ratio между разными уровнями сети от типичных для резнетов к практикующимся в трансформерах. На уровне количества блоков в резнете это переход от (3,4,6,3) блоков на каждом этапе (stage) резнета к (3,3,9,3). Это повышает качество бейзлайна с 78.8% до 79.4%.
Также ствол сети делают более похожим на трансформерный и вместо агрессивного даунсемплинга резнетов делают что-то больше похожее на “патчификацию” трансформеров (свёртки 4x4 с шагом 4, то есть изображение распадается на непересекающиеся патчи). Это даёт буст с 79.4% до 79.5%.
2. ResNeXt-ификация.
В свёрточных моделях ResNeXt (https://arxiv.org/abs/1611.05431) использовались групповые свёртки (grouped convolution) и увеличенная ширина сети. Предельный случай групповых свёрток это depthwise свёртки, где число групп равно числу каналов (кажется, стали популярны после модели Xception (https://arxiv.org/abs/1610.02357) от, неожиданно, широко известного Франсуа Шолле, автора Кераса и нашумевшей статьи про измерение интеллекта). В данной работе берут depthwise свёртки и увеличивают ширину сети, это даёт буст до 80.5%.
3. Инвертированный боттлнек.
В резнетах классика жанра это уменьшение размерности каналов через 1x1 свёртку, вычисление более тяжёлой свёртки (обычно 3x3) на том что получилось, и снова восстановление размерности. В трансформерах же всё наоборот, внутри FFN слоя происходит расширение размерности вместо сжатия, это и есть inverted bottleneck. Здесь это тоже делают, получают 80.6%.
4. Большие ядра свёрток.
Zhuang Liu, Hanzi Mao, Chao-Yuan Wu, Christoph Feichtenhofer, Trevor Darrell, Saining Xie
Статья: https://arxiv.org/abs/2201.03545
Код: https://github.com/facebookresearch/ConvNeXt (нормально так, что у несколькодневной репы уже 1.7К звёзд)
Империя наносит алаверды.
После всех этих историй с заменой свёрточных сетей на трансформеры (ViT, https://www.tgoop.com/gonzo_ML/434), а затем на старые добрые полносвязные сети (https://www.tgoop.com/gonzo_ML/800), явно должно было быть что-то ответное от свёрточных сетей в духе, что вы их готовить не умеете. И вот, пожалуйста :)
Свежая работа от 10 января 2022 из главного центра экспертизы по свёрточным сетям им. Яна Лекуна (FAIR) + Беркли.
Это снова история и про то, нужны все эти inductive biases или нет, в них соль или нет. Польза от inductive biases свёрточных сетей, особенно translation equivariance, очевидно, есть, раз значительная доля продвинутых модификаций трансформеров и MLP ушла в сторону гибридизации и привнесения свойств свёрток в эти модели. А если так, то может достаточно и свёрточных моделей, раз в них уже всё нужное есть?
Авторы поступили просто — взяли стандартный ResNet и постепенно прошли путь, добавляя в него разные вещи, показавшие себя хорошо в трансформерах (сохраняя при этом количество вычислений на примерно одинаковом уровне, чтобы было честно). И добились таки чисто свёрточной архитектуры (ConvNeXt), бьющей лучшие имеющиеся трансформеры аналогичных размеров (имеется в виду Swin Transformer, https://github.com/microsoft/Swin-Transformer).
В качестве объектов берут сети двух размеров ResNet-50/Swin-T и ResNet-200/Swin-B, также оценивают скейлинг на модели размера XL, но дальше не идут, так что сравниться напрямую со Swin V2 (https://arxiv.org/abs/2111.09883) размеров H и G не получится.
Во-первых, начальные резнеты обучают аналогичными ViT процедурами, и это само по себе уже даёт повышение качества (Top-1 accuracy на ImageNet) с 76.1% до 78.8% для ResNet-50. Сюда входит много всяких изменений и улучшений: 300 эпох вместо 90, оптимизатор AdamW, аугментации через Mixup, Cutmix, RandAugment, Random Erasing, регуляризации включая stochastic depth и label smoothing. Если вы с чем-то из этого ещё не знакомы и всё ещё кипятите, то это хороший повод набраться актуальных рецептов. В статье все ссылки есть.
Дальше изменения бьются на несколько блоков.
1. Макро дизайн.
Тут изменяют соотношение compute ratio между разными уровнями сети от типичных для резнетов к практикующимся в трансформерах. На уровне количества блоков в резнете это переход от (3,4,6,3) блоков на каждом этапе (stage) резнета к (3,3,9,3). Это повышает качество бейзлайна с 78.8% до 79.4%.
Также ствол сети делают более похожим на трансформерный и вместо агрессивного даунсемплинга резнетов делают что-то больше похожее на “патчификацию” трансформеров (свёртки 4x4 с шагом 4, то есть изображение распадается на непересекающиеся патчи). Это даёт буст с 79.4% до 79.5%.
2. ResNeXt-ификация.
В свёрточных моделях ResNeXt (https://arxiv.org/abs/1611.05431) использовались групповые свёртки (grouped convolution) и увеличенная ширина сети. Предельный случай групповых свёрток это depthwise свёртки, где число групп равно числу каналов (кажется, стали популярны после модели Xception (https://arxiv.org/abs/1610.02357) от, неожиданно, широко известного Франсуа Шолле, автора Кераса и нашумевшей статьи про измерение интеллекта). В данной работе берут depthwise свёртки и увеличивают ширину сети, это даёт буст до 80.5%.
3. Инвертированный боттлнек.
В резнетах классика жанра это уменьшение размерности каналов через 1x1 свёртку, вычисление более тяжёлой свёртки (обычно 3x3) на том что получилось, и снова восстановление размерности. В трансформерах же всё наоборот, внутри FFN слоя происходит расширение размерности вместо сжатия, это и есть inverted bottleneck. Здесь это тоже делают, получают 80.6%.
4. Большие ядра свёрток.
GitHub
GitHub - facebookresearch/ConvNeXt: Code release for ConvNeXt model
Code release for ConvNeXt model. Contribute to facebookresearch/ConvNeXt development by creating an account on GitHub.
https://arxiv.org/abs/2103.05524
On the interplay between data structure and loss function in classification problems (NIPS 2021)
Using methods from statistical physics, we obtain a precise asymptotic expression for the train and test errors of random feature models trained on a simple model of structured data. The input covariance is built from independent blocks allowing us to tune the saliency of low-dimensional structures and their alignment with respect to the target function.Our results show in particular that in the over-parametrized regime, the impact of data structure on both train and test error curves is greater for logistic loss than for mean-squared loss: the easier the task, the wider the gap in performance between the two losses at the advantage of the logistic. Numerical experiments on MNIST and CIFAR10 confirm our insights.
On the interplay between data structure and loss function in classification problems (NIPS 2021)
Using methods from statistical physics, we obtain a precise asymptotic expression for the train and test errors of random feature models trained on a simple model of structured data. The input covariance is built from independent blocks allowing us to tune the saliency of low-dimensional structures and their alignment with respect to the target function.Our results show in particular that in the over-parametrized regime, the impact of data structure on both train and test error curves is greater for logistic loss than for mean-squared loss: the easier the task, the wider the gap in performance between the two losses at the advantage of the logistic. Numerical experiments on MNIST and CIFAR10 confirm our insights.
https://ieeexplore.ieee.org/document/9381694
Hausdorff GAN
Data usually resides on a manifold, and the minimal dimension of such a manifold is called its intrinsic dimension. This fundamental data property is not considered in the generative adversarial network (GAN) model along with its its variants; such that original data and generated data often hold different intrinsic dimensions. The different intrinsic dimensions of both generated and original data may cause generated data distribution to not match original data distribution completely, and it certainly will hurt the quality of generated data. In this study, we first show that GAN is often unable to generate simulation data, holding the same intrinsic dimension as the original data with both theoretical analysis and experimental illustration. Next, we propose a new model, called Hausdorff GAN, which removes the issue of different intrinsic dimensions and introduces the Hausdorff metric into GAN training to generate higher quality data.
Hausdorff GAN
Data usually resides on a manifold, and the minimal dimension of such a manifold is called its intrinsic dimension. This fundamental data property is not considered in the generative adversarial network (GAN) model along with its its variants; such that original data and generated data often hold different intrinsic dimensions. The different intrinsic dimensions of both generated and original data may cause generated data distribution to not match original data distribution completely, and it certainly will hurt the quality of generated data. In this study, we first show that GAN is often unable to generate simulation data, holding the same intrinsic dimension as the original data with both theoretical analysis and experimental illustration. Next, we propose a new model, called Hausdorff GAN, which removes the issue of different intrinsic dimensions and introduces the Hausdorff metric into GAN training to generate higher quality data.
Probabilistic_Deep_Learning_With_Python,_Keras_and_TensorFlow_Probability.pdf
19.2 MB
There are two powerful probabilistic principles: maximum likelihood and Bayes. Maximum likelihood (fondly referred to as MaxLike) governs all traditional DL. Understanding networks as probabilistic models trained with the maximum likelihood principle helps you to boost the performance of your networks (as Google did when going from WaveNet to WaveNet++) or to generate astounding applications (like OpenAI did with Glow, a net that generates realistic looking faces). Bayesian methods come into play in situations where networks need to say, “I’m not sure.” (Strangely, traditional NNs cannot do this.) The subtitle for the book, “with Python, Keras, and TensorFlow Probability,” reflects the fact that you really should get your hands dirty and do some coding
Intrinsic Dimensionality Explains the Effectiveness of Language Model Fine-Tuning https://arxiv.org/abs/2012.13255
Although pretrained language models can be fine-tuned to produce state-of-the-art results for a very wide range of language understanding tasks, the dynamics of this process are not well understood, especially in the low data regime. Why can we use relatively vanilla gradient descent algorithms (e.g., without strong regularization) to tune a model with hundreds of millions of parameters on datasets with only hundreds or thousands of labeled examples? In this paper, we argue that analyzing fine-tuning through the lens of intrinsic dimension provides us with empirical and theoretical intuitions to explain this remarkable phenomenon. We empirically show that common pre-trained models have a very low intrinsic dimension; in other words, there exists a low dimension reparameterization that is as effective for fine-tuning as the full parameter space.
Although pretrained language models can be fine-tuned to produce state-of-the-art results for a very wide range of language understanding tasks, the dynamics of this process are not well understood, especially in the low data regime. Why can we use relatively vanilla gradient descent algorithms (e.g., without strong regularization) to tune a model with hundreds of millions of parameters on datasets with only hundreds or thousands of labeled examples? In this paper, we argue that analyzing fine-tuning through the lens of intrinsic dimension provides us with empirical and theoretical intuitions to explain this remarkable phenomenon. We empirically show that common pre-trained models have a very low intrinsic dimension; in other words, there exists a low dimension reparameterization that is as effective for fine-tuning as the full parameter space.
🔥1
https://arxiv.org/abs/1911.11775
Improving Polyphonic Music Models with Feature-Rich Encoding
This paper explores sequential modelling of polyphonic music with deep neural networks. While recent breakthroughs have focussed on network architecture, we demonstrate that the representation of the sequence can make an equally significant contribution to the performance of the model as measured by validation set loss. By extracting salient features inherent to the training dataset, the model can either be conditioned on these features or trained to predict said features as extra components of the sequences being modelled. We show that training a neural network to predict a seemingly more complex sequence, with extra features included in the series being modelled, can improve overall model performance significantly. We first introduce TonicNet, a GRU-based model trained to initially predict the chord at a given time-step before then predicting the notes of each voice at that time-step, in contrast with the typical approach of predicting only the notes. We then evaluate TonicNet on the canonical JSB Chorales dataset and obtain state-of-the-art results.
Improving Polyphonic Music Models with Feature-Rich Encoding
This paper explores sequential modelling of polyphonic music with deep neural networks. While recent breakthroughs have focussed on network architecture, we demonstrate that the representation of the sequence can make an equally significant contribution to the performance of the model as measured by validation set loss. By extracting salient features inherent to the training dataset, the model can either be conditioned on these features or trained to predict said features as extra components of the sequences being modelled. We show that training a neural network to predict a seemingly more complex sequence, with extra features included in the series being modelled, can improve overall model performance significantly. We first introduce TonicNet, a GRU-based model trained to initially predict the chord at a given time-step before then predicting the notes of each voice at that time-step, in contrast with the typical approach of predicting only the notes. We then evaluate TonicNet on the canonical JSB Chorales dataset and obtain state-of-the-art results.
👍1
Д. Б. Фукс, Классические многообразия
Главным ингредиентом систем образующих оказываются скручивания Дена — диффеоморфизмы Fg —> Pg состоящие в разрезании одной из ручек по меридиану со склеиванием после поворота на 360°
http://www.mathnet.ru/links/f89a177f93b8c2404273b232b8ec7655/intf71.pdf
Главным ингредиентом систем образующих оказываются скручивания Дена — диффеоморфизмы Fg —> Pg состоящие в разрезании одной из ручек по меридиану со склеиванием после поворота на 360°
http://www.mathnet.ru/links/f89a177f93b8c2404273b232b8ec7655/intf71.pdf
👍1🔥1🫡1
Geometric and Physical Quantities Improve E(3) Equivariant Message Passing
Including covariant information, such as position, force, velocity or spin is important in many tasks in computational physics and chemistry. We introduce Steerable E(3) Equivariant Graph Neural Networks (SEGNNs) that generalise equivariant graph networks, such that node and edge attributes are not restricted to invariant scalars, but can contain covariant information, such as vectors or tensors. This model, composed of steerable MLPs, is able to incorporate geometric and physical information in both the message and update functions. Through the definition of steerable node attributes, the MLPs provide a new class of activation functions for general use with steerable feature fields. We discuss ours and related work through the lens of equivariant non-linear convolutions, which further allows us to pin-point the successful components of SEGNN.
https://arxiv.org/abs/2110.02905
Including covariant information, such as position, force, velocity or spin is important in many tasks in computational physics and chemistry. We introduce Steerable E(3) Equivariant Graph Neural Networks (SEGNNs) that generalise equivariant graph networks, such that node and edge attributes are not restricted to invariant scalars, but can contain covariant information, such as vectors or tensors. This model, composed of steerable MLPs, is able to incorporate geometric and physical information in both the message and update functions. Through the definition of steerable node attributes, the MLPs provide a new class of activation functions for general use with steerable feature fields. We discuss ours and related work through the lens of equivariant non-linear convolutions, which further allows us to pin-point the successful components of SEGNN.
https://arxiv.org/abs/2110.02905
Geodesic complexity of homogeneous Riemannian manifolds
We study the geodesic motion planning problem for complete Riemannian manifolds and investigate their geodesic complexity, an integer-valued isometry invariant introduced by D. Recio-Mitter. Using methods from Riemannian geometry, we establish new lower and upper bounds on geodesic complexity and compute its value for certain classes of examples with a focus on homogeneous Riemannian manifolds. Methodically, we study properties of stratifications of cut loci and use results on their structures for certain homogeneous manifolds obtained by T. Sakai and others.
https://arxiv.org/abs/2105.09215
We study the geodesic motion planning problem for complete Riemannian manifolds and investigate their geodesic complexity, an integer-valued isometry invariant introduced by D. Recio-Mitter. Using methods from Riemannian geometry, we establish new lower and upper bounds on geodesic complexity and compute its value for certain classes of examples with a focus on homogeneous Riemannian manifolds. Methodically, we study properties of stratifications of cut loci and use results on their structures for certain homogeneous manifolds obtained by T. Sakai and others.
https://arxiv.org/abs/2105.09215
Universality Theorems for Generative Models
Despite the fact that generative models are extremely successful in practice, the theory underlying this phenomenon is only starting to catch up with practice. In this work we address the question of the universality of generative models: is it true that neural networks can approximate any data manifold arbitrarily well? We provide a positive answer to this question and show that under mild assumptions on the activation function one can always find a feedforward neural network which maps the latent space onto a set located within the specified Hausdorff distance from the desired data manifold. We also prove similar theorems for the case of multiclass generative models and cycle generative models, trained to map samples from one manifold to another and vice versa
https://arxiv.org/abs/1905.11520
Despite the fact that generative models are extremely successful in practice, the theory underlying this phenomenon is only starting to catch up with practice. In this work we address the question of the universality of generative models: is it true that neural networks can approximate any data manifold arbitrarily well? We provide a positive answer to this question and show that under mild assumptions on the activation function one can always find a feedforward neural network which maps the latent space onto a set located within the specified Hausdorff distance from the desired data manifold. We also prove similar theorems for the case of multiclass generative models and cycle generative models, trained to map samples from one manifold to another and vice versa
https://arxiv.org/abs/1905.11520
Triangulation complexity and systolic volume of hyperbolic manifolds
Let M be a closed n-manifold with nonzero simplicial volume. A central result in systolic geometry from Gromov is that systolic volume of M is related to its simplicial volume. In this short note, we show that systolic volume of hyperbolic manifolds is related to triangulation complexity. The proof is based on Jørgensen and Thurston's theorem of hyperbolic volume.
https://arxiv.org/abs/2109.09194
Let M be a closed n-manifold with nonzero simplicial volume. A central result in systolic geometry from Gromov is that systolic volume of M is related to its simplicial volume. In this short note, we show that systolic volume of hyperbolic manifolds is related to triangulation complexity. The proof is based on Jørgensen and Thurston's theorem of hyperbolic volume.
https://arxiv.org/abs/2109.09194
😱1
Forwarded from MAA — САП
О главном результате САП 2021-го года. В 70-х годах А.К. Боусфильд показал, что вторые гомологии пронильпотетного пополнения свободной нециклической группы H_2(F^) несчетны. Его доказательство использовало симплициальные методы и спектральную последовательность Квиллена. Долгое время в направлении исследований гомологий пронильпотетных пополнений не появлялось никаких новых результатов. В 2017-м году С. Иванов и Р. Михайлов решили известную проблему Боусфильда, построив конечное Q-плохое пространство, и с помощью тех же самых методов показали, что H_2(F^) не является делимой группой. Ничего больше о группе H_2(F^) не было известно, а любое новое утверждение о ней, представляет, несомненный интерес.
Разница между гомологиями обратных пределов и обратными пределами гомологий описывается для многих случаев и категорий. Эта разница оказывается lim^1 -- производным пределом от последовательности групп. Возникает естественный вопрос: а можно ли получить подобный результат для гомологий групп? В частности, представляется ли H_2(F^) как lim^1 от некоторой последовательности групп? В недавней работе Барнеа и Шелаха подобное доказывается для первых гомологий групп. Если есть обратная последовательность эпиморфизмов, то разница между первыми гомологиями обратного предела и обратным пределом первых гомологий, оказывается некоторым lim^1. Напомним, что абелева группа представима как некоторый lim^1 тогда и только тогда, когда она является кокручением. Есть несколько эквивалентных определений кокручения и вышеупомянутое свойство также можно рассматривать как одно из определений.
Является ли группа H_2(F^) кокручением? Это задача, над которой работали сотрудники лаборатории в течении долгого времени. Методы, развитые в ранних работах С. Иванова и Р. Михайлова, оказались недостаточными для вывода или опровержения подобного результата. Кокручение является тонким и сложно-уловимым свойством. Оказалось, что для решения этой задачи необходимо привлечение принципиально новых методов, больше относящихся к анализу, нежели к алгебре и топологии, что удивительно и представляет собой редкий случай подобного взаимодействия областей.
В итоге, М. Б., С. И. и Р. М. показали, что H_2(F^) не является кокручением. Доказательство приведено в работе
https://arxiv.org/abs/2107.01485
и представляет собой на данный момент самое сложное рассуждение из всего, что есть в этой области. Это главный результат, полученный в САП в 2021-м году.
Разница между гомологиями обратных пределов и обратными пределами гомологий описывается для многих случаев и категорий. Эта разница оказывается lim^1 -- производным пределом от последовательности групп. Возникает естественный вопрос: а можно ли получить подобный результат для гомологий групп? В частности, представляется ли H_2(F^) как lim^1 от некоторой последовательности групп? В недавней работе Барнеа и Шелаха подобное доказывается для первых гомологий групп. Если есть обратная последовательность эпиморфизмов, то разница между первыми гомологиями обратного предела и обратным пределом первых гомологий, оказывается некоторым lim^1. Напомним, что абелева группа представима как некоторый lim^1 тогда и только тогда, когда она является кокручением. Есть несколько эквивалентных определений кокручения и вышеупомянутое свойство также можно рассматривать как одно из определений.
Является ли группа H_2(F^) кокручением? Это задача, над которой работали сотрудники лаборатории в течении долгого времени. Методы, развитые в ранних работах С. Иванова и Р. Михайлова, оказались недостаточными для вывода или опровержения подобного результата. Кокручение является тонким и сложно-уловимым свойством. Оказалось, что для решения этой задачи необходимо привлечение принципиально новых методов, больше относящихся к анализу, нежели к алгебре и топологии, что удивительно и представляет собой редкий случай подобного взаимодействия областей.
В итоге, М. Б., С. И. и Р. М. показали, что H_2(F^) не является кокручением. Доказательство приведено в работе
https://arxiv.org/abs/2107.01485
и представляет собой на данный момент самое сложное рассуждение из всего, что есть в этой области. Это главный результат, полученный в САП в 2021-м году.
🔥1
Geometrically Enriched Latent Spaces
A common assumption in generative models is that the generator immerses the latent space into a Euclidean ambient space. Instead, we consider the ambient space to be a Riemannian manifold, which allows for encoding domain knowledge through the associated Riemannian metric. Shortest paths can then be defined accordingly in the latent space to both follow the learned manifold and respect the ambient geometry. Through careful design of the ambient metric we can ensure that shortest paths are well-behaved even for deterministic generators that otherwise would exhibit a misleading bias. Experimentally we show that our approach improves interpretability of learned representations both using stochastic and deterministic generators.
https://arxiv.org/abs/2008.00565
A common assumption in generative models is that the generator immerses the latent space into a Euclidean ambient space. Instead, we consider the ambient space to be a Riemannian manifold, which allows for encoding domain knowledge through the associated Riemannian metric. Shortest paths can then be defined accordingly in the latent space to both follow the learned manifold and respect the ambient geometry. Through careful design of the ambient metric we can ensure that shortest paths are well-behaved even for deterministic generators that otherwise would exhibit a misleading bias. Experimentally we show that our approach improves interpretability of learned representations both using stochastic and deterministic generators.
https://arxiv.org/abs/2008.00565
🤯1
Understanding Overparameterization in Generative Adversarial Networks
In this work, we present a comprehensive analysis of the importance of model overparameterization in GANs both theoretically and empirically. We theoretically show that in an overparameterized GAN model with a 1-layer neural network generator and a linear discriminator, GDA converges to a global saddle point of the underlying non-convex concave min-max problem. To the best of our knowledge, this is the first result for global convergence of GDA in such settings. Our theory is based on a more general result that holds for a broader class of nonlinear generators and discriminators that obey certain assumptions (including deeper generators and random feature discriminators). We also empirically study the role of model overparameterization in GANs using several large-scale experiments on CIFAR-10 and Celeb-A datasets.
https://arxiv.org/abs/2104.05605
In this work, we present a comprehensive analysis of the importance of model overparameterization in GANs both theoretically and empirically. We theoretically show that in an overparameterized GAN model with a 1-layer neural network generator and a linear discriminator, GDA converges to a global saddle point of the underlying non-convex concave min-max problem. To the best of our knowledge, this is the first result for global convergence of GDA in such settings. Our theory is based on a more general result that holds for a broader class of nonlinear generators and discriminators that obey certain assumptions (including deeper generators and random feature discriminators). We also empirically study the role of model overparameterization in GANs using several large-scale experiments on CIFAR-10 and Celeb-A datasets.
https://arxiv.org/abs/2104.05605
🤯1