Forwarded from Олимпиадная математика ВсОШ | Дабромат
⬜️ Финал олимпиады им. Шарыгина
Олимпиада имени И.Ф Шарыгина — это престижная геометрическая олимпиада для школьников 8–10 классов. Организатором выступает МЦНМО (Московский центр непрерывного математического образования).
Игорь Фёдорович Шарыгин — советский и российский математик и педагог, специалист по элементарной геометрии, популяризатор науки, автор учебников и пособий для школьников.
После окончания механико-математического факультета Московского государственного университета, Шарыгин остался в аспирантуре, а затем начал свою педагогическую карьеру в МГУ.
На протяжении многих лет Игорь Федорович посвятил себя не только преподаванию, но и популяризации математики. Он стал автором множества учебников и методических пособий, которые пользовались огромной популярностью и использовались в школах по всей стране.
В память об Игоре Фёдоровиче Шарыгине ряд российских научных организаций и учебных заведений решили ежегодно, начиная с 2005 года, проводить геометрическую олимпиаду.
Финальный тур 20-й олимпиады им. Шарыгина состоялся 30 июля - 2 августа. На решение задач участникам 8-10 классов отводилось два дня: 31 июля и 1 августа.
На сайте вы можете посмотреть с задания прошлых лет, а мы делимся с вами условиями этого года.
В комментариях можно найти решения👇🏻
Олимпиада имени И.Ф Шарыгина — это престижная геометрическая олимпиада для школьников 8–10 классов. Организатором выступает МЦНМО (Московский центр непрерывного математического образования).
Игорь Фёдорович Шарыгин — советский и российский математик и педагог, специалист по элементарной геометрии, популяризатор науки, автор учебников и пособий для школьников.
После окончания механико-математического факультета Московского государственного университета, Шарыгин остался в аспирантуре, а затем начал свою педагогическую карьеру в МГУ.
На протяжении многих лет Игорь Федорович посвятил себя не только преподаванию, но и популяризации математики. Он стал автором множества учебников и методических пособий, которые пользовались огромной популярностью и использовались в школах по всей стране.
В память об Игоре Фёдоровиче Шарыгине ряд российских научных организаций и учебных заведений решили ежегодно, начиная с 2005 года, проводить геометрическую олимпиаду.
Финальный тур 20-й олимпиады им. Шарыгина состоялся 30 июля - 2 августа. На решение задач участникам 8-10 классов отводилось два дня: 31 июля и 1 августа.
На сайте вы можете посмотреть с задания прошлых лет, а мы делимся с вами условиями этого года.
В комментариях можно найти решения👇🏻
✍20👍6🔥2❤1
Говорят, стартовала Летняя конференция Турнира Городов. Там есть классный геометрический проект про точки Шиффлера. Пока традиционно проект выложен не весь. Не знаю как вам, а мне прям интересно! Планирую пару вечеров посидеть-порешать. У проекта появился свой телеграм-канал, в котором, видимо, будут публиковаться иллюстрации к задачам и комментарии.
Что такое точка Шиффлера? Помните я как-то писал тут про факт, что если у четырех треугольников ABC, BCD, CDA и DAB три из прямых Эйлера проходят через одну точку, то и четвертая проходит через эту же точку. Так вот, если точка D=I — инцентр треугольника, то как раз выполняются условия и точка пересечения называется точкой Шиффлера треугольника. ГМТ точек D, для которых выполнено свойство, кстати, тоже по-своему интересно: оно состоит из описанной окружности треугольника, бесконечно удаленной прямой и кубики Нойберга.
В честь кого названа точка? Точка названа в честь любителя геометрии Курта Шиффлера, 1896-1996, (см. фото), основателя фирмы, которая специализируется на производстве игрушек, мебели и учебных материалов для детских садов.
Что такое точка Шиффлера? Помните я как-то писал тут про факт, что если у четырех треугольников ABC, BCD, CDA и DAB три из прямых Эйлера проходят через одну точку, то и четвертая проходит через эту же точку. Так вот, если точка D=I — инцентр треугольника, то как раз выполняются условия и точка пересечения называется точкой Шиффлера треугольника. ГМТ точек D, для которых выполнено свойство, кстати, тоже по-своему интересно: оно состоит из описанной окружности треугольника, бесконечно удаленной прямой и кубики Нойберга.
В честь кого названа точка? Точка названа в честь любителя геометрии Курта Шиффлера, 1896-1996, (см. фото), основателя фирмы, которая специализируется на производстве игрушек, мебели и учебных материалов для детских садов.
❤28🔥5🥰4✍2👍2🤯2❤🔥1🤝1
Forwarded from Математические кружки | «МТ кружки»
Новая 15-я задачная разминка «Поиск клада» — от нашего преподавателя Фёдора Львовича Бахарева. Его лаконичный комментарий:
Иногда задачи по геометрии имеют шутливую форму, но от этого не перестают быть содержательными. Наша первая разминка в этом сезоне — шуточно-геометрическая!
Будем рады увидеть в комментариях ваши решения или просто мысли о задачах!
Разбор задач будет проводиться Фёдором Львовичем в пятницу 9 августа в 18:00 мск по ссылке https://us06web.zoom.us/j/5634707332?pwd=TUcxTlJQbmxxMGRucDJ0ejVDaVZ3UT09&omn=83695771588
Присоединяйтесь!
#мт_разминка_продолжающие
Подписаться на «Математические кружки»
Please open Telegram to view this post
VIEW IN TELEGRAM
👍10❤3✍2
Одно из главных умений, которому надо научиться начинающему геометру, это понимать какие объекты на картинке зависят друг от друга, а какие нет. Зачастую это позволяет априори установить, что какой-то один угол выражается через какой-то другой, и на основании этого придумывать решение.
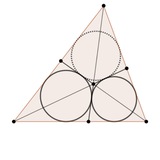
Одна из моих любимых задач на эту тему такая: доказать, что красные отрезки на картинке равны тогда и только тогда, когда равны синие.
Кидайте в комментариях задачи, где полезно разделить зависимости между объектами на картинке!
Одна из моих любимых задач на эту тему такая: доказать, что красные отрезки на картинке равны тогда и только тогда, когда равны синие.
Кидайте в комментариях задачи, где полезно разделить зависимости между объектами на картинке!
❤43👍12🥰9🔥7✍3💯1
Меня тут опять перепутали с другим Федором. На этот раз с Федей П. Это, конечно, очень лестно для меня, но теперь количество Федоров, с которыми меня можно перепутать, не столь уж велико. Если вы все еще нас путаете, то решите классическую задачу не по геометрии, придуманную задолго до того, как путать Федоров стало мэйнстримом.
😁81🔥6👍4💊2❤1🕊1🌚1
Я вот думаю, что если есть какое-то разумное утверждение про окружность, то оно должно быть в каком-то смысле верно и для равнобокой гиперболы.
На картинке треугольник описан около равнобокой гиперболы. Прямую, соединяющую две точки касания, пересекли с прямой, соединяющей третью с центром гиперболы. Докажите, что точка пересечения лежит на медиане треугольника.
На картинке треугольник описан около равнобокой гиперболы. Прямую, соединяющую две точки касания, пересекли с прямой, соединяющей третью с центром гиперболы. Докажите, что точка пересечения лежит на медиане треугольника.
☃19👍5🔥5❤4😱3
Forwarded from Иван Олейник
Приветствую. Заметил интересный факт: вершина треугольника A, соответствующая ей точка Шалтая P, симметричная A относительно точки Фейербаха A' и центр вписанной окружности I лежат на одной окружности. Предполагаю, что это известное утверждение. Буду признателен, если поделитесь интересными решениями.
🔥22👍4🎄4✍2
Forwarded from NeuroGeometry (Петр Ким)
Хотели бы сделать объявление:
С 18 по 23 августа на аопсе (ссылка ниже) будет проходить очень интересная олимпиада MGO 2024.
Составители задач - очень опытные геометры, среди них есть:
- Жюри олимпиады Шарыгина
- Золотые медалисты уровня Advanced Иранской геометрической Олимпиады
- Победители SAGF и Discord Geometry Olympiad
- Победители ВСОШ и кандидаты в сборную России на Международную Математическую Олимпиаду
Сложность задач будет достаточно высока: по шкале Imo Shortlist:
p1/p4 - G4
p2/p5 - G6/G7
p3/p6 - G8+
При этом в отличии от других олимпиад по геометрии высокой сложности на этой олимпиаде не будет:
- нагромождённых конструкций (все условия не более 4 строк в длину и обладают поразительной красотой)
- сложных объектов (каких-нибудь никому не известных замечательных точек, коник, или кубик)
- геометрических неравенств или комбинаторной геометрии
От себя могу добавить, что на мой взгляд, на этой олимпиаде будет несколько задач, которые могут претендовать на звание самых красивых задач в истории. Всем рекомендую поучаствовать!
https://artofproblemsolving.com/community/c594864h3379839_mgo_2024_announced
С 18 по 23 августа на аопсе (ссылка ниже) будет проходить очень интересная олимпиада MGO 2024.
Составители задач - очень опытные геометры, среди них есть:
- Жюри олимпиады Шарыгина
- Золотые медалисты уровня Advanced Иранской геометрической Олимпиады
- Победители SAGF и Discord Geometry Olympiad
- Победители ВСОШ и кандидаты в сборную России на Международную Математическую Олимпиаду
Сложность задач будет достаточно высока: по шкале Imo Shortlist:
p1/p4 - G4
p2/p5 - G6/G7
p3/p6 - G8+
При этом в отличии от других олимпиад по геометрии высокой сложности на этой олимпиаде не будет:
- нагромождённых конструкций (все условия не более 4 строк в длину и обладают поразительной красотой)
- сложных объектов (каких-нибудь никому не известных замечательных точек, коник, или кубик)
- геометрических неравенств или комбинаторной геометрии
От себя могу добавить, что на мой взгляд, на этой олимпиаде будет несколько задач, которые могут претендовать на звание самых красивых задач в истории. Всем рекомендую поучаствовать!
https://artofproblemsolving.com/community/c594864h3379839_mgo_2024_announced
❤🔥41🎉5❤3🤡1
Про точку Шалтая тетраэдра можно думать так.
Пусть дан тетраэдр ABCD. Рассмотрим три сферы, касающиеся грани BCD в точках B, C и D и проходящие через вершину A. Докажите, что точка пересечения этих сфер, отличная от A, лежит на сфере, симметричной описанной около ABCD относительно грани BCD.
А какие еще свойства есть у такой точки?
Пусть дан тетраэдр ABCD. Рассмотрим три сферы, касающиеся грани BCD в точках B, C и D и проходящие через вершину A. Докажите, что точка пересечения этих сфер, отличная от A, лежит на сфере, симметричной описанной около ABCD относительно грани BCD.
А какие еще свойства есть у такой точки?
❤26👍5🤔4😁3
Forwarded from Олимпиадная математика ВсОШ | Дабромат
Пришло время познакомить вас с «ядром» каждой ступени курса, руководителями направлений, которые будут составлять план занятий, координировать работу преподавателей и ассистентов, чтобы механизм курса работал слаженно.
Со всей информацией можно ознакомиться в карточках, а про ступени — подробнее узнать на нашем сайте.
Со всей информацией можно ознакомиться в карточках, а про ступени — подробнее узнать на нашем сайте.
❤18🔥5🥰5🐳1
Forwarded from Геометрия-канал (Grigory Merzon)
а) Четырехугольник вписан в конику и описан вокруг коники. Теорема Понселе говорит, что тогда четырехугольник можно “вращать” с сохранением вписанности и описанности. Доказать, что точки пересечения противоположных сторон всё время лежат на одной прямой.
б) Полный четырехсторонник вписан в кубику и описан вокруг коники. Доказать, что четырехсторонник можно “вращать” с сохранением вписанности и описанности (предыдущий пункт соответствует кубике, распадающейся в объединение коники и прямой).
// via П.Бибиков: https://vk.com/wall840911_606
б) Полный четырехсторонник вписан в кубику и описан вокруг коники. Доказать, что четырехсторонник можно “вращать” с сохранением вписанности и описанности (предыдущий пункт соответствует кубике, распадающейся в объединение коники и прямой).
// via П.Бибиков: https://vk.com/wall840911_606
🤯19🔥7👍3❤2
сумма длин перпендикуляров из точки на стороны многоугольника Понселе не меняется
geometry_ukraine
Geometry Trip
https://youtu.be/QiaB6zubVws?si=LQCaWfTWMpUdLy6r
geometry_ukraine
Geometry Trip
https://youtu.be/QiaB6zubVws?si=LQCaWfTWMpUdLy6r
YouTube
Poncelet altitudes #geometry #maths #геометрія #geogebra
Works for an arbitrary blue point and for an arbitrary bicentric n-gon.
🔥16❤4🥰2
Forwarded from Фулл и точка
Наш проект развивается после завершения конференции 🤟
Публикуем запись лекции про проективные коники.
🐴🐴🐴🐴🐴🐴🐴🐴🐴🐴🐴
Разговор про коники не только интересен, но еще и полезен!
Многие задачи по геометрии (в частности, с различных олимпиад) имеют очень короткое и естественное решение, использующее коники, несмотря на то, что кониками в их условии даже не пахнет 🤯
Яркий пример тому есть в нашем проекте — самое простое доказательство существования точки Шиффлера обычными методами занимает страницу текста, а вот при помощи равнобоких гипербол это делается буквально в одну строчку 🤩
Многих пугает новая теория, но бояться не стоит. Мы сделали так, чтобы разговор про коники был доступен каждому, кто увлекается обычной планиметрией)
Заваривайте себе кружечку горячего чая и кликайте сюда 👉 тык-тык 👈
Публикуем запись лекции про проективные коники.
🐴🐴🐴🐴🐴🐴🐴🐴🐴🐴🐴
Разговор про коники не только интересен, но еще и полезен!
Многие задачи по геометрии (в частности, с различных олимпиад) имеют очень короткое и естественное решение, использующее коники, несмотря на то, что кониками в их условии даже не пахнет 🤯
Яркий пример тому есть в нашем проекте — самое простое доказательство существования точки Шиффлера обычными методами занимает страницу текста, а вот при помощи равнобоких гипербол это делается буквально в одну строчку 🤩
Многих пугает новая теория, но бояться не стоит. Мы сделали так, чтобы разговор про коники был доступен каждому, кто увлекается обычной планиметрией)
Заваривайте себе кружечку горячего чая и кликайте сюда 👉 тык-тык 👈
YouTube
Проективные коники | Точка Шиффлера | Летняя Конференция Турнира Городов | @tournamentoftowns
Лекция "Проективные коники" для части 4 на проекте "Точка Шиффлера" Летней Конференции Турнира Городов
#maths #math #mathematics #geometry #математика #геометрия
Тайм-коды:
0:00:00 - Заставка
0:01:29 - Введение в проективную геометрию
0:14:05 - Проективные…
#maths #math #mathematics #geometry #математика #геометрия
Тайм-коды:
0:00:00 - Заставка
0:01:29 - Введение в проективную геометрию
0:14:05 - Проективные…
🔥28❤5👍4💩2
Forwarded from Геометрия-канал (Grigory Merzon)
Для окружности радиус в точку касания перпендикулярен касательной.
А что для эллипса: как связаны отрезок из фокуса в точку касания и перпендикуляр из фокуса на касательную? Простая задача: доказать, что красные отрезки параллельны.
// via Д.А.Терёшин via Stanley Rabinowitz
А что для эллипса: как связаны отрезок из фокуса в точку касания и перпендикуляр из фокуса на касательную? Простая задача: доказать, что красные отрезки параллельны.
// via Д.А.Терёшин via Stanley Rabinowitz
❤15✍2🤡2👍1💩1