Forwarded from Фулл и точка
В Сириусе в эти дни проходит отбор кандидатов в национальную сборную России по математике 💪
Сегодня в рамках отборочных мероприятий состоялась очень серьезная Sirius Mathematical Olympiad 🧐
Представляем вашему вниманию первую задачу второго дня этой олимпиады 🔥
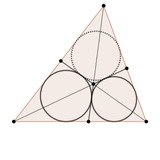
Задача. По высотам остроугольного неравнобедренного треугольника из его вершин одновременно начали ползти три жука с одинаковыми скоростями.
В некоторый момент оказалось, что первый и второй жук находятся на вписанной в треугольник окружности. Докажите, что в этот момент и третий жук тоже находится на этой окружности 🪲🐞
Условия олимпиады можете найти в канале главного тренера сборной России Кирилла Андреевича Сухова 😎
Сегодня в рамках отборочных мероприятий состоялась очень серьезная Sirius Mathematical Olympiad 🧐
Представляем вашему вниманию первую задачу второго дня этой олимпиады 🔥
Задача. По высотам остроугольного неравнобедренного треугольника из его вершин одновременно начали ползти три жука с одинаковыми скоростями.
В некоторый момент оказалось, что первый и второй жук находятся на вписанной в треугольник окружности. Докажите, что в этот момент и третий жук тоже находится на этой окружности 🪲🐞
Условия олимпиады можете найти в канале главного тренера сборной России Кирилла Андреевича Сухова 😎
❤31❤🔥6👍6✍3🔥3
Несколько месяцев назад Tran Quang Hung придумал классную задачу и прислал ее мне, сказав, что Алексей Заславский придумал к ней счетное решение в барицентрических координатах. Я ему в ответ послал относительное геометрическое решение...
Сейчас автор планирует опубликовать ее на аопсе, так что я не вижу препятствий к публикации у себя на канале.
Шалтай-Болтайная ось треугольника ABC отрезает от него треугольник ADE. Докажите, что Шалтай-Ботайная ось ADE параллельна BC.
Сейчас автор планирует опубликовать ее на аопсе, так что я не вижу препятствий к публикации у себя на канале.
Шалтай-Болтайная ось треугольника ABC отрезает от него треугольник ADE. Докажите, что Шалтай-Ботайная ось ADE параллельна BC.
😁39👏7❤3🔥3🤯3✍2❤🔥1👍1
Forwarded from Tournament of Towns
Осенний тур 46го Турнира городов состоялся!
На сайте Турнира опубликованы условия сложного варианта, прошедшего в это воскресенье!
The autumn round of the 46th Tournament of Towns was successfully held!
Problems of the A-level, that took place this Sunday, are already published on the website.
#осеннийтур #46турниргородов
#46tournamentoftowns
На сайте Турнира опубликованы условия сложного варианта, прошедшего в это воскресенье!
The autumn round of the 46th Tournament of Towns was successfully held!
Problems of the A-level, that took place this Sunday, are already published on the website.
#осеннийтур #46турниргородов
#46tournamentoftowns
❤12👍1👏1
Гайз (энд гёрлз)! Регистрация на JetBrains Youth Challenge наконец-то открылась!
Напоминаю, что математическая командная олимпиада состоится уже 17-го ноября сего года!
Нам прислали кучу супер красивой и сложной геометрии, хоть отдельное соревнование устраивай, ну и всего остального по чуть-чуть, так что вариант обещает быть жарким, по части геометрии так точно.
На всякий случай, напомню, что в математических командах может быть от 1 до 3 человек, а соревнование проводится в двух возрастных категориях (проверяйте на входе, сеньоры вы или юниоры). Дополнительный челлендж — олимпиада проводится на английском языке и она устная, впрочем в прошлом году некоторые команды решали этот вопрос творчески и с юмором! Прямо поставил бы дополнительные баллы за находчивость!
Еще один дополнительный челлендж для некоторых локаций — олимпиада проводится в Дискорде. Но тут, я надеюсь, находчивость вам тоже поможет. Если вы не знаете, как побороть технические трудности, а поучаствовать вы ооочень хотите, то мы придумаем, как вам помочь.
На какой уровень сложности задач надо ориентироваться? Это очень тонкий вопрос... В прошлом году мы слегонца недооценили то, какие сильные команды придут к нам, поэтому в этом году мы планируем перестраховаться и дать задачи посложнее в конец варианта.
Короче, будем рады вас видеть на нашей олимпиаде.
Устная командная олимпиада по математике на ломаном английском в Дискорде это круто и весело!
Напоминаю, что математическая командная олимпиада состоится уже 17-го ноября сего года!
Нам прислали кучу супер красивой и сложной геометрии, хоть отдельное соревнование устраивай, ну и всего остального по чуть-чуть, так что вариант обещает быть жарким, по части геометрии так точно.
На всякий случай, напомню, что в математических командах может быть от 1 до 3 человек, а соревнование проводится в двух возрастных категориях (проверяйте на входе, сеньоры вы или юниоры). Дополнительный челлендж — олимпиада проводится на английском языке и она устная, впрочем в прошлом году некоторые команды решали этот вопрос творчески и с юмором! Прямо поставил бы дополнительные баллы за находчивость!
Еще один дополнительный челлендж для некоторых локаций — олимпиада проводится в Дискорде. Но тут, я надеюсь, находчивость вам тоже поможет. Если вы не знаете, как побороть технические трудности, а поучаствовать вы ооочень хотите, то мы придумаем, как вам помочь.
На какой уровень сложности задач надо ориентироваться? Это очень тонкий вопрос... В прошлом году мы слегонца недооценили то, какие сильные команды придут к нам, поэтому в этом году мы планируем перестраховаться и дать задачи посложнее в конец варианта.
Короче, будем рады вас видеть на нашей олимпиаде.
Устная командная олимпиада по математике на ломаном английском в Дискорде это круто и весело!
JetBrains: Developer Tools for Professionals and Teams
JetBrains Academy Youth Challenge
Ultimate coding and math challenge for the school students from JetBrains Academy
❤27❤🔥6🔥6🤡4👍1🤮1
This media is not supported in your browser
VIEW IN TELEGRAM
Поризм Брокара. Все шесть углов имеют фиксированную величину
2❤🔥61❤20👍12🤯7🤮5🔥2
segments.pdf
128.8 KB
Еще один листик для начинающих. Вообще таких зада очень и очень много и их очень любят давать на олимпиадах младших классов, но именно в этот листик вошло всего восемь задач...
2👍28🆒7
Forwarded from Ботаем геому
Условия прошедшей сегодня устной олимпиады по геометрии!
Если писали тур, расскажите, какие задачи вам понравились/не понравились.
Решения появятся в течении следующей недели
Если писали тур, расскажите, какие задачи вам понравились/не понравились.
Решения появятся в течении следующей недели
❤🔥32❤11👍11
Всем привет! Трудно себе представить, что вы подписаны на какой-нибудь геометрический канал и еще не слышали про спецкурс Ивана Кухарчука. Но все-таки, все-таки... если вы еще не слышали...
Живая классика это не какой-то элитный жилой комплекс в центре Москвы, а геометрический спецкурс Ивана Кухарчука на платфоме Дабромат! Там будут всякие классические сюжеты, которые пока еще не стали достаточно популярными среди задачных композиторов и решателей, несмотря на их классичность... Это будет без сомнения интересно и качественно!
Если бы мне заплатили за эту рекламу, то я без сомнения потратил эти деньги на спецкурс Живая классика!
Живая классика это не какой-то элитный жилой комплекс в центре Москвы, а геометрический спецкурс Ивана Кухарчука на платфоме Дабромат! Там будут всякие классические сюжеты, которые пока еще не стали достаточно популярными среди задачных композиторов и решателей, несмотря на их классичность... Это будет без сомнения интересно и качественно!
Если бы мне заплатили за эту рекламу, то я без сомнения потратил эти деньги на спецкурс Живая классика!
👎85🥰28😁8🤡6👍4🔥4❤2
Слишком много дизлайков... Вот вам тогда задача с командной олимпиады проходящего сейчас Уральского турнира (63-го? я сбился со счета...)
CM — медиана равнобедренного остроугольного треугольника ABC (AB = BC). Точка D на отрезке CM такова, что AD — внешняя биссектриса угла MDB. Точка E на отрезке CM такова, что CE = BD. Докажите, что BE = AD.
CM — медиана равнобедренного остроугольного треугольника ABC (AB = BC). Точка D на отрезке CM такова, что AD — внешняя биссектриса угла MDB. Точка E на отрезке CM такова, что CE = BD. Докажите, что BE = AD.
👍75❤9👎8😍6🥱2🗿2🦄2👾1
А вот кстати, завтра закроется регистрация на математический курс от Jet Brains. За три недели мы там поговорили про многочлены в целом, про разностный многочлен и вычисление разных сумм, про интерполяцию. Сейчас у нас первая неделя комбинаторного (дискретно-вероятностного) блока. И в нем мы дали одну, кажется, довольно трудную задачу. На вчерашний день ее правильно решил только один человек... из 400 зарегистрировавшихся на курсе (ну ладно, кого я обманываю, из 80-ти активно решающих). В конце недели опубликую эту задачу в комбинаторном канале (@olympcomba)...
JetBrains: Developer Tools for Professionals and Teams
JetBrains Youth Math Club
A free online Math club for high-schoolers from JetBrains
🥰6👍4❤2❤🔥2🖕1
Forwarded from Олимпиадная математика ВсОШ | Дабромат
Первый человек, решивший задачу верно, получит возможность обучаться на «Живой Классике» абсолютно бесплатно, а следующим 5 счастливчикам будет предоставлена скидка 50% на покупку спецкурса! 🤑
Как сдать задачу?
Конечно же через Таксу Дусю! Это ваш главный виртуальный помощник, который будет сопровождать вас на протяжение всего обучения.
Отправляйте решение задачи, и бот передаст их преподавателям, которые, в свою очередь, дадут фидбэк в течение 24 часов. Кстати, на нашем основном курсе ребята тоже получают комментарии в течение одного дня.
Что еще умеет Дуся?
🐶 Такса Дуся — многофункциональный бот и умеет не только принимать задачи, но и много чего еще:
🐾 Предоставляет подсказки и мотивацию, если вы столкнулись с трудностями в решении задач.
🐾 Напоминает об эфирах. Не упустите важные онлайн-разборы и лекции — Дуся заранее уведомит вас о них.
🐾 Информирует о новостях. Оставайтесь в курсе последних событий, включая анонсы новых курсов и других мероприятий.
🐾 Отвечает на вопросы по условиям задач. Если у вас возникли сложности с пониманием задания, Дуся свяжет вас с преподавателем или ассистентом для получения необходимой помощи.
🐾 Показывает личный рейтинг. Следите за своим прогрессом, чтобы постоянно стремиться к новым достижениям.
🐾 Помогает родителям отслеживать успеваемость. Родители могут в один клик получить отчеты о достижениях своего ребенка.
Скорее решайте задачку и скидывайте ее Дусе — не упустите возможность стать участником спецкурса бесплатно!
Как сдать задачу?
Конечно же через Таксу Дусю! Это ваш главный виртуальный помощник, который будет сопровождать вас на протяжение всего обучения.
Отправляйте решение задачи, и бот передаст их преподавателям, которые, в свою очередь, дадут фидбэк в течение 24 часов. Кстати, на нашем основном курсе ребята тоже получают комментарии в течение одного дня.
Что еще умеет Дуся?
🐶 Такса Дуся — многофункциональный бот и умеет не только принимать задачи, но и много чего еще:
🐾 Предоставляет подсказки и мотивацию, если вы столкнулись с трудностями в решении задач.
🐾 Напоминает об эфирах. Не упустите важные онлайн-разборы и лекции — Дуся заранее уведомит вас о них.
🐾 Информирует о новостях. Оставайтесь в курсе последних событий, включая анонсы новых курсов и других мероприятий.
🐾 Отвечает на вопросы по условиям задач. Если у вас возникли сложности с пониманием задания, Дуся свяжет вас с преподавателем или ассистентом для получения необходимой помощи.
🐾 Показывает личный рейтинг. Следите за своим прогрессом, чтобы постоянно стремиться к новым достижениям.
🐾 Помогает родителям отслеживать успеваемость. Родители могут в один клик получить отчеты о достижениях своего ребенка.
Скорее решайте задачку и скидывайте ее Дусе — не упустите возможность стать участником спецкурса бесплатно!
😭23❤10✍3💩3🤡3👍2🔥2❤🔥1👎1
Forwarded from Геометрия-канал (knamprihodilinoneseichas knamprihodilinoneseichas)
USEMO 2024 P3. Автор: Matsvei Zorka.
Докажите равенство зеленых.
Докажите равенство зеленых.
1🔥43👍4😈2🖕1
Так-так-так... Разыскиваются сильные команды, способные решить все задачи на JetBrains Math Challenge! Мне кажется, что в этот раз это будет не так просто... До окончания регистрации осталась всего неделя! А до самой олимпиады всего две недели (чуть меньше)!
(Кстати, это хороший способ потренироваться перед Колмом...)
(Кстати, это хороший способ потренироваться перед Колмом...)
JetBrains: Developer Tools for Professionals and Teams
JetBrains Academy Youth Challenge
Ultimate coding and math challenge for the school students from JetBrains Academy
🥰14❤6👏4👎2😁2❤🔥1👍1🖕1💊1