Куда поехать летом?
С 4 по 28 августа 2025 в Армении 🇦🇲 пройдет летняя школа "Лес" 🌳
🌲 На школе 4 направления:
📈 Математическое,
🔭 Физическое,
📚 Гуманитарное,
🍀 Биологическое.
Проект не про подготовку к олимпиадам или поступление — основная цель получить удовольствие от научных сюжетов и общения в атмосфере настоящего палаточного лагеря.
Хотя основной набор уже закрыт, подать заявку всё ещё можно! 🙂
P. S. Карточки по оригами помогла нам сделать Полина Романова —одна из преподавателей летней школы 🔥
С 4 по 28 августа 2025 в Армении 🇦🇲 пройдет летняя школа "Лес" 🌳
🌲 На школе 4 направления:
📈 Математическое,
🔭 Физическое,
📚 Гуманитарное,
🍀 Биологическое.
Проект не про подготовку к олимпиадам или поступление — основная цель получить удовольствие от научных сюжетов и общения в атмосфере настоящего палаточного лагеря.
Хотя основной набор уже закрыт, подать заявку всё ещё можно! 🙂
P. S. Карточки по оригами помогла нам сделать Полина Романова —одна из преподавателей летней школы 🔥
#геом_разминка
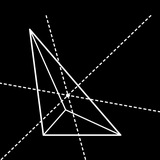
Задача. Каждая из сторон 𝐴𝐵 и 𝐶𝐷 выпуклого четырёхугольника 𝐴𝐵𝐶𝐷 разделена на три равные части, 𝐴𝐸 = 𝐸𝐹 = 𝐹𝐵, 𝐷𝑃 = 𝑃𝑄 = 𝑄𝐶. Диагонали 𝐴𝐸𝑃𝐷 и 𝐹𝐵𝐶𝑄 пересекаются в точках 𝑀 и 𝑁 соответственно. Докажите, что сумма площадей треугольников 𝐴𝑀𝐷 и 𝐵𝑁𝐶 равна сумме площадей треугольников 𝐸𝑃𝑀 и 𝐹𝑁𝑄.
Задача. Каждая из сторон 𝐴𝐵 и 𝐶𝐷 выпуклого четырёхугольника 𝐴𝐵𝐶𝐷 разделена на три равные части, 𝐴𝐸 = 𝐸𝐹 = 𝐹𝐵, 𝐷𝑃 = 𝑃𝑄 = 𝑄𝐶. Диагонали 𝐴𝐸𝑃𝐷 и 𝐹𝐵𝐶𝑄 пересекаются в точках 𝑀 и 𝑁 соответственно. Докажите, что сумма площадей треугольников 𝐴𝑀𝐷 и 𝐵𝑁𝐶 равна сумме площадей треугольников 𝐸𝑃𝑀 и 𝐹𝑁𝑄.
#геом_разминка
Задача. Пусть 𝐴𝐵𝐶 — прямоугольный треугольник с углом 𝐴 = 90°, точка 𝐷 — основание высоты из 𝐴 на 𝐵𝐶, а 𝐸 — средина 𝐷𝐶. Окружность 𝐴𝐵𝐷 вторично пересекает 𝐴𝐸 в точке 𝐹. Пусть 𝑋 — это пересечение прямых 𝐴𝐵 и 𝐷𝐹. Докажите, что 𝑋𝐷 = 𝑋𝐶.
Задача. Пусть 𝐴𝐵𝐶 — прямоугольный треугольник с углом 𝐴 = 90°, точка 𝐷 — основание высоты из 𝐴 на 𝐵𝐶, а 𝐸 — средина 𝐷𝐶. Окружность 𝐴𝐵𝐷 вторично пересекает 𝐴𝐸 в точке 𝐹. Пусть 𝑋 — это пересечение прямых 𝐴𝐵 и 𝐷𝐹. Докажите, что 𝑋𝐷 = 𝑋𝐶.
#геом_разминка
Угадайте где мы?📍
Задача. Пусть 𝐴𝐵𝐶 остроугольный треугольник, 𝑘 — его описанная окружность с центром 𝑂. Прямая, проходящая через 𝑂 пересекает стороны 𝐴𝐵 и 𝐴𝐶 в точках 𝐷 и 𝐸 соответственно. Пусть 𝐵′ и 𝐶′ — симметрии 𝐵 и 𝐶 относительно 𝑂 соответственно. Докажите, что (𝑂𝐷𝐶′) и (𝑂𝐸𝐵′) пересекаются на 𝑘.
Доброго утра и прекрасного настроения 🥰
Угадайте где мы?
Задача. Пусть 𝐴𝐵𝐶 остроугольный треугольник, 𝑘 — его описанная окружность с центром 𝑂. Прямая, проходящая через 𝑂 пересекает стороны 𝐴𝐵 и 𝐴𝐶 в точках 𝐷 и 𝐸 соответственно. Пусть 𝐵′ и 𝐶′ — симметрии 𝐵 и 𝐶 относительно 𝑂 соответственно. Докажите, что (𝑂𝐷𝐶′) и (𝑂𝐸𝐵′) пересекаются на 𝑘.
Доброго утра и прекрасного настроения 🥰
Please open Telegram to view this post
VIEW IN TELEGRAM
#геом_разминка
Задача. Пусть 𝐴𝐵𝐶 — остроугольный неравнобедренный треугольник с центром описанной окружности 𝑂. Пусть 𝐷 — основание высоты из 𝐴 на сторону 𝐵𝐶. Прямые 𝐵𝐶 и 𝐴𝑂 пересекаются в точке 𝐸. Пусть 𝑠 — прямая, проходящая через 𝐸 перпендикулярно 𝐴𝑂. Прямая 𝑠 пересекает 𝐴𝐵 и 𝐴𝐶 в точках 𝐾 и 𝐿 соответственно. Обозначим через 𝜔 описанную окружность треугольника 𝐴𝐾𝐿. Прямая 𝐴𝐷 вторично пересекает 𝜔 в точке 𝑋. Докажите, что 𝜔 и описанные окружности треугольников 𝐴𝐵𝐶 и 𝐷𝐸𝑋 имеют общую точку.
Задача. Пусть 𝐴𝐵𝐶 — остроугольный неравнобедренный треугольник с центром описанной окружности 𝑂. Пусть 𝐷 — основание высоты из 𝐴 на сторону 𝐵𝐶. Прямые 𝐵𝐶 и 𝐴𝑂 пересекаются в точке 𝐸. Пусть 𝑠 — прямая, проходящая через 𝐸 перпендикулярно 𝐴𝑂. Прямая 𝑠 пересекает 𝐴𝐵 и 𝐴𝐶 в точках 𝐾 и 𝐿 соответственно. Обозначим через 𝜔 описанную окружность треугольника 𝐴𝐾𝐿. Прямая 𝐴𝐷 вторично пересекает 𝜔 в точке 𝑋. Докажите, что 𝜔 и описанные окружности треугольников 𝐴𝐵𝐶 и 𝐷𝐸𝑋 имеют общую точку.
#геом_разминка #красота_спасет_мир
Задача. В четырехугольнике 𝐴𝐵𝐶𝐷 с ∠𝐵𝐴𝐷 = ∠𝐵𝐶𝐷 диагональ 𝐴𝐶 пересекает описанную окружность 𝐵𝐶𝐷 в точке 𝑃 отличной от 𝐶. Пусть 𝑄, 𝑅, 𝑆 и 𝑇 — симметрии 𝑃 относительно 𝐴𝐵, 𝐵𝐶, 𝐶𝐷 и 𝐷𝐴 соответственно. Докажите, что описанная окружность треугольника 𝐴𝑄𝑇 касается прямой 𝑅𝑆.
Задача. В четырехугольнике 𝐴𝐵𝐶𝐷 с ∠𝐵𝐴𝐷 = ∠𝐵𝐶𝐷 диагональ 𝐴𝐶 пересекает описанную окружность 𝐵𝐶𝐷 в точке 𝑃 отличной от 𝐶. Пусть 𝑄, 𝑅, 𝑆 и 𝑇 — симметрии 𝑃 относительно 𝐴𝐵, 𝐵𝐶, 𝐶𝐷 и 𝐷𝐴 соответственно. Докажите, что описанная окружность треугольника 𝐴𝑄𝑇 касается прямой 𝑅𝑆.
#геом_разминка
Задача. Пусть 𝐴𝐵𝐶 — треугольник с центром вписанной окружности 𝐼, а 𝑀 — середина 𝐵𝐶. Луч 𝑀𝐼 пересекает 𝐴𝐵 и 𝐴𝐶 в точках 𝑃 и 𝑄. Если 𝑁 — середина большей дуги 𝐵𝐶, докажите, что центр описанной окружности треугольника 𝑁𝑃𝑄 лежит на 𝐴𝐼.
Задача. Пусть 𝐴𝐵𝐶 — треугольник с центром вписанной окружности 𝐼, а 𝑀 — середина 𝐵𝐶. Луч 𝑀𝐼 пересекает 𝐴𝐵 и 𝐴𝐶 в точках 𝑃 и 𝑄. Если 𝑁 — середина большей дуги 𝐵𝐶, докажите, что центр описанной окружности треугольника 𝑁𝑃𝑄 лежит на 𝐴𝐼.
#геом_разминка
Задача. Пусть 𝐴𝐵𝐶 — равнобедренный треугольник с 𝐴𝐵 = 𝐴𝐶. Пусть 𝑃 — точка на описанной окружности треугольника 𝐴𝐵𝐶, и пусть 𝑋 и 𝑌 — основания перпендикуляров из 𝑃 на 𝐴𝐵 и 𝐴𝐶, соответственно. Пусть 𝐴′ — точка, диаметрально противоположная 𝐴 на описанной окружности 𝐴𝐵𝐶. Пусть 𝑇 — точка пересечения прямой 𝑃𝐴′ с прямой 𝐵𝐶, и пусть 𝐻 — ортоцентр треугольника 𝐴𝐵𝐶. Докажите, что 𝑇𝐻 ‖ 𝑋𝑌.
Задача. Пусть 𝐴𝐵𝐶 — равнобедренный треугольник с 𝐴𝐵 = 𝐴𝐶. Пусть 𝑃 — точка на описанной окружности треугольника 𝐴𝐵𝐶, и пусть 𝑋 и 𝑌 — основания перпендикуляров из 𝑃 на 𝐴𝐵 и 𝐴𝐶, соответственно. Пусть 𝐴′ — точка, диаметрально противоположная 𝐴 на описанной окружности 𝐴𝐵𝐶. Пусть 𝑇 — точка пересечения прямой 𝑃𝐴′ с прямой 𝐵𝐶, и пусть 𝐻 — ортоцентр треугольника 𝐴𝐵𝐶. Докажите, что 𝑇𝐻 ‖ 𝑋𝑌.
This media is not supported in your browser
VIEW IN TELEGRAM
#геом_разминка
Публикуем задачу с прошедшего вчера первого тура Туймаады 🐿
Задача. Окружности 𝜔₁ и 𝜔₂ проходят через точку 𝐴 и касаются прямой ℓ в точках 𝐵₁ и 𝐵₂ соответственно. Переменная прямая 𝑚 проходит через точку 𝐴 и вторично пересекает окружности 𝜔₁ и 𝜔₂ в (переменных) точках 𝑃₁ и 𝑃₂ соответственно. Лучи 𝑃₁𝐵₁ и 𝑃₂𝐵₂ пересекаются в точке 𝑃. Докажите, что касательная в точке 𝑃 к описанной окружности треугольника 𝑃𝑃₁𝑃₂ проходит через точку, не зависящую от выбора прямой 𝑚.
Публикуем задачу с прошедшего вчера первого тура Туймаады 🐿
Задача. Окружности 𝜔₁ и 𝜔₂ проходят через точку 𝐴 и касаются прямой ℓ в точках 𝐵₁ и 𝐵₂ соответственно. Переменная прямая 𝑚 проходит через точку 𝐴 и вторично пересекает окружности 𝜔₁ и 𝜔₂ в (переменных) точках 𝑃₁ и 𝑃₂ соответственно. Лучи 𝑃₁𝐵₁ и 𝑃₂𝐵₂ пересекаются в точке 𝑃. Докажите, что касательная в точке 𝑃 к описанной окружности треугольника 𝑃𝑃₁𝑃₂ проходит через точку, не зависящую от выбора прямой 𝑚.
Выбираем лучшую геому
Anonymous Poll
21%
Младшие №2. Равные диагонали
17%
Младшие №8. Центры на одной прямой
22%
Старшие №2. Фиксированная точка
40%
Старшие №7. Отражения относ. сторон
#геом_разминка
Предлагаем вашему вниманию упражнение, возникшее в качестве вспомогательного у одного из участников Туймаады. Как из него следует решение задачи мл-2?
Задача. Дан четырехугольник 𝐴𝐵𝐶𝐷 с точкой пересечения диагоналей 𝑃. Окружность, проходящая через точку 𝐵 и касающаяся прямой 𝐴𝐶 в точке 𝐴, пересекает прямую 𝐵𝐷 вторично в точке 𝑋. Окружность, проходящая через точку 𝐶 и касающаяся прямой 𝐵𝐷 в точке 𝐷, пересекает прямую 𝐴𝐶 вторично в точке 𝑌. Пусть также 𝐴𝑍 и 𝐷𝑇 — биссектрисы треугольников 𝑋𝐴𝐵 и 𝑌𝐷𝐶 соответственно. Докажите, что 𝑍𝑇 = 𝐴𝐷.
Предлагаем вашему вниманию упражнение, возникшее в качестве вспомогательного у одного из участников Туймаады. Как из него следует решение задачи мл-2?
Задача. Дан четырехугольник 𝐴𝐵𝐶𝐷 с точкой пересечения диагоналей 𝑃. Окружность, проходящая через точку 𝐵 и касающаяся прямой 𝐴𝐶 в точке 𝐴, пересекает прямую 𝐵𝐷 вторично в точке 𝑋. Окружность, проходящая через точку 𝐶 и касающаяся прямой 𝐵𝐷 в точке 𝐷, пересекает прямую 𝐴𝐶 вторично в точке 𝑌. Пусть также 𝐴𝑍 и 𝐷𝑇 — биссектрисы треугольников 𝑋𝐴𝐵 и 𝑌𝐷𝐶 соответственно. Докажите, что 𝑍𝑇 = 𝐴𝐷.
#разминка
Задача. По кругу стоят 2025 человек, каждый из которых либо рыцарь, который всегда говорит правду, либо лжец, который всегда лжёт. Каждый из этих 2025 человек сказал: Среди меня, двух моих соседей слева и двух соседей справа ровно три рыцаря. Какое наибольшее количество рыцарей может быть среди этих людей?
Задача. По кругу стоят 2025 человек, каждый из которых либо рыцарь, который всегда говорит правду, либо лжец, который всегда лжёт. Каждый из этих 2025 человек сказал: Среди меня, двух моих соседей слева и двух соседей справа ровно три рыцаря. Какое наибольшее количество рыцарей может быть среди этих людей?