#геом_разминка #easy #9
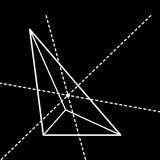
Задача. Пусть 𝐴𝐵𝐶𝐷 — вписанный четырёхугольник и 𝐸 — точка пересечения прямых 𝐴𝐵 и 𝐶𝐷. На сторонах 𝐶𝐷 и 𝐴𝐵 взяты точки 𝐾 и 𝐿 соответственно, удовлетворяющие условиям ∠𝐾𝐴𝐷 = ∠𝐾𝐵𝐶 и ∠𝐿𝐷𝐴 = ∠𝐿𝐶𝐵. Докажите, что 𝐸𝐾 = 𝐸𝐿.
Задача. Пусть 𝐴𝐵𝐶𝐷 — вписанный четырёхугольник и 𝐸 — точка пересечения прямых 𝐴𝐵 и 𝐶𝐷. На сторонах 𝐶𝐷 и 𝐴𝐵 взяты точки 𝐾 и 𝐿 соответственно, удовлетворяющие условиям ∠𝐾𝐴𝐷 = ∠𝐾𝐵𝐶 и ∠𝐿𝐷𝐴 = ∠𝐿𝐶𝐵. Докажите, что 𝐸𝐾 = 𝐸𝐿.
❤16🔥3👍2🥰2🐳2
#геом_разминка #medium #9
Задача. На стороне 𝐴𝐶 треугольника 𝐴𝐵𝐶 с углом ∠𝐶 < ∠𝐴 < 90° выбрана точка 𝐷 так, что 𝐵𝐷 = 𝐵𝐴. Вписанная окружность треугольника 𝐴𝐵𝐶 касается 𝐴𝐵 и 𝐴𝐶 в точках 𝐾 и 𝐿 соответственно. Пусть 𝐽 — центр вписанной окружности треугольника 𝐵𝐶𝐷. Докажите, что прямая 𝐾𝐿 пересекает отрезок 𝐴𝐽 по его середине.
Задача. На стороне 𝐴𝐶 треугольника 𝐴𝐵𝐶 с углом ∠𝐶 < ∠𝐴 < 90° выбрана точка 𝐷 так, что 𝐵𝐷 = 𝐵𝐴. Вписанная окружность треугольника 𝐴𝐵𝐶 касается 𝐴𝐵 и 𝐴𝐶 в точках 𝐾 и 𝐿 соответственно. Пусть 𝐽 — центр вписанной окружности треугольника 𝐵𝐶𝐷. Докажите, что прямая 𝐾𝐿 пересекает отрезок 𝐴𝐽 по его середине.
🔥7❤4❤🔥2
#геом_разминка #medium #8
Задача. На сторонах выпуклого четырехугольника 𝐴𝐵𝐶𝐷 во внутреннюю сторону (см. картинку) построены правильные треугольники. Оказалось, что треугольники, построенные на 𝐴𝐵 и 𝐶𝐷, имеют общую вершину 𝑀. Докажите, что два других построенных правильных треугольника имеют общий центр.
Задача. На сторонах выпуклого четырехугольника 𝐴𝐵𝐶𝐷 во внутреннюю сторону (см. картинку) построены правильные треугольники. Оказалось, что треугольники, построенные на 𝐴𝐵 и 𝐶𝐷, имеют общую вершину 𝑀. Докажите, что два других построенных правильных треугольника имеют общий центр.
❤8👍3❤🔥2🔥1
#геом_разминка #easy #8
Задача. Дан параллелограмм 𝐴𝐵𝐶𝐷 и точки 𝐸 и 𝐹 на его сторонах 𝐴𝐵 и 𝐴𝐷 соответственно. Прямая 𝐸𝐹 пересекает прямые 𝐵𝐶 и 𝐶𝐷 в точках 𝑃 и 𝑄 соответственно. Докажите, что площади треугольников 𝑃𝐴𝑄 и 𝐸𝐶𝐹 равны.
Задача. Дан параллелограмм 𝐴𝐵𝐶𝐷 и точки 𝐸 и 𝐹 на его сторонах 𝐴𝐵 и 𝐴𝐷 соответственно. Прямая 𝐸𝐹 пересекает прямые 𝐵𝐶 и 𝐶𝐷 в точках 𝑃 и 𝑄 соответственно. Докажите, что площади треугольников 𝑃𝐴𝑄 и 𝐸𝐶𝐹 равны.
❤10🔥3👍2🥰2👾1
#геом_разминка #medium #9
Задача. На стороне 𝐴𝐶 треугольника 𝐴𝐵𝐶 отмечена такая точка 𝐸, что ∠𝐵𝐸𝐶 = ∠𝐴𝐵𝐶. На продолжении отрезка 𝐵𝐸 за точку 𝐸 отмечена такая точка 𝐷, что ∠𝐵𝐶𝐸 = ∠𝐶𝐷𝐸. На отрезке 𝐴𝐵 отмечена такая точка 𝐹, что 𝐵𝐹 = 𝐶𝐷. Докажите, что прямая 𝐵𝐶 касается описанной окружности треугольника 𝐴𝐹𝐶.
Задача. На стороне 𝐴𝐶 треугольника 𝐴𝐵𝐶 отмечена такая точка 𝐸, что ∠𝐵𝐸𝐶 = ∠𝐴𝐵𝐶. На продолжении отрезка 𝐵𝐸 за точку 𝐸 отмечена такая точка 𝐷, что ∠𝐵𝐶𝐸 = ∠𝐶𝐷𝐸. На отрезке 𝐴𝐵 отмечена такая точка 𝐹, что 𝐵𝐹 = 𝐶𝐷. Докажите, что прямая 𝐵𝐶 касается описанной окружности треугольника 𝐴𝐹𝐶.
❤8✍3👍2🔥2
#геом_разминка #medium #10
Задача. Пусть 𝜔 — полуокружность с диаметром 𝑋𝑌. Пусть 𝑀 — середина 𝑋𝑌. Пусть 𝐴 — произвольная точка на 𝜔, такая, что 𝐴𝑋 < 𝐴𝑌. Пусть 𝐵 и 𝐶 — точки, лежащие на отрезках 𝑋𝑀 и 𝑌𝑀 соответственно, такие, что 𝐵𝑀 = 𝐶𝑀. Прямая, проходящая через 𝐶 параллельно 𝐴𝐵, пересекает 𝜔 в точке 𝑃. Прямая, проходящая через 𝐵 параллельно 𝐴𝐶, пересекает 𝜔 в точке 𝑄. Прямая 𝑃𝑄 пересекает прямую 𝑋𝑌 в точке 𝑆. Докажите, что прямая 𝐴𝑆 касается 𝜔.
Задача. Пусть 𝜔 — полуокружность с диаметром 𝑋𝑌. Пусть 𝑀 — середина 𝑋𝑌. Пусть 𝐴 — произвольная точка на 𝜔, такая, что 𝐴𝑋 < 𝐴𝑌. Пусть 𝐵 и 𝐶 — точки, лежащие на отрезках 𝑋𝑀 и 𝑌𝑀 соответственно, такие, что 𝐵𝑀 = 𝐶𝑀. Прямая, проходящая через 𝐶 параллельно 𝐴𝐵, пересекает 𝜔 в точке 𝑃. Прямая, проходящая через 𝐵 параллельно 𝐴𝐶, пересекает 𝜔 в точке 𝑄. Прямая 𝑃𝑄 пересекает прямую 𝑋𝑌 в точке 𝑆. Докажите, что прямая 𝐴𝑆 касается 𝜔.
❤9🔥2🥰1
#на_ночь_глядя поздравляем всех с Днем Чебурашки 🍊
Иван Андреевич — один из авторов нашего канала — вместе с Артемием Алексеевичем Соколовым придумали прикольную задачку, которая потом была на Турнире Городов. Ни на что не намекаем, но чертеж кого-то напоминает :)
Задача. Даны две равные окружности 𝜔₁ и 𝜔₂ с центрами 𝑂₁ и 𝑂₂. На отрезке 𝑂₁𝑂₂ взяты точки 𝑋 и 𝑌 так, что 𝑂₁𝑌 = 𝑂₂𝑋. Точки 𝐴 и 𝐵 лежат на 𝜔₁, и прямая 𝐴𝐵 проходит через 𝑋. Точки 𝐶 и 𝐷 лежат на 𝜔₂, и прямая 𝐶𝐷 проходит через 𝑌 . Докажите, что существует окружность, касающаяся прямых 𝐴𝑂₁, 𝐵𝑂₁, 𝐶𝑂₂ и 𝐷𝑂₂.
Иван Андреевич — один из авторов нашего канала — вместе с Артемием Алексеевичем Соколовым придумали прикольную задачку, которая потом была на Турнире Городов. Ни на что не намекаем, но чертеж кого-то напоминает :)
Задача. Даны две равные окружности 𝜔₁ и 𝜔₂ с центрами 𝑂₁ и 𝑂₂. На отрезке 𝑂₁𝑂₂ взяты точки 𝑋 и 𝑌 так, что 𝑂₁𝑌 = 𝑂₂𝑋. Точки 𝐴 и 𝐵 лежат на 𝜔₁, и прямая 𝐴𝐵 проходит через 𝑋. Точки 𝐶 и 𝐷 лежат на 𝜔₂, и прямая 𝐶𝐷 проходит через 𝑌 . Докажите, что существует окружность, касающаяся прямых 𝐴𝑂₁, 𝐵𝑂₁, 𝐶𝑂₂ и 𝐷𝑂₂.
😁17❤5❤🔥3🔥3🍌2🍓1
#геом_разминка #medium #9
Задача. Пусть отрезок 𝐴𝐵 — диаметр полуокружности ℎ. На ℎ лежит точка 𝐶, отличная от точек 𝐴 и 𝐵. Пусть 𝐷 — основание перпендикуляра из 𝐶 на 𝐴𝐵. Окружность 𝑘 лежит вне треугольника 𝐴𝐷𝐶 и одновременно касается полуокружности ℎ и отрезков 𝐴𝐵 и 𝐶𝐷. Пусть 𝐸 — точка касания окружности 𝑘 с прямой 𝐴𝐵. Докажите, что 𝐴𝐶 = 𝐴𝐸.
Задача. Пусть отрезок 𝐴𝐵 — диаметр полуокружности ℎ. На ℎ лежит точка 𝐶, отличная от точек 𝐴 и 𝐵. Пусть 𝐷 — основание перпендикуляра из 𝐶 на 𝐴𝐵. Окружность 𝑘 лежит вне треугольника 𝐴𝐷𝐶 и одновременно касается полуокружности ℎ и отрезков 𝐴𝐵 и 𝐶𝐷. Пусть 𝐸 — точка касания окружности 𝑘 с прямой 𝐴𝐵. Докажите, что 𝐴𝐶 = 𝐴𝐸.
❤9❤🔥2🔥2
#геом_разминка #medium #9
Задача. Пусть 𝐴𝐵𝐶 — треугольник с описанной окружностью Γ. Пусть 𝑃 и 𝑄 — точки в той полуплоскости от 𝐵𝐶, что содержит 𝐴, такие, что 𝐵𝑃 и 𝐶𝑄 являются касательными к Γ, и 𝑃𝐵 = 𝐵𝐶 = 𝐶𝑄. Пусть 𝐾 и 𝐿 — точки на внешней биссектрисе угла ∠𝐶𝐴𝐵, такие, что 𝐵𝐾 = 𝐵𝐴, 𝐶𝐿 = 𝐶𝐴. Пусть 𝑀 — точка пересечения прямых 𝑃𝐾 и 𝑄𝐿. Докажите, что 𝑀𝐾 = 𝑀𝐿.
Задача. Пусть 𝐴𝐵𝐶 — треугольник с описанной окружностью Γ. Пусть 𝑃 и 𝑄 — точки в той полуплоскости от 𝐵𝐶, что содержит 𝐴, такие, что 𝐵𝑃 и 𝐶𝑄 являются касательными к Γ, и 𝑃𝐵 = 𝐵𝐶 = 𝐶𝑄. Пусть 𝐾 и 𝐿 — точки на внешней биссектрисе угла ∠𝐶𝐴𝐵, такие, что 𝐵𝐾 = 𝐵𝐴, 𝐶𝐿 = 𝐶𝐴. Пусть 𝑀 — точка пересечения прямых 𝑃𝐾 и 𝑄𝐿. Докажите, что 𝑀𝐾 = 𝑀𝐿.
❤4🔥4❤🔥2👍2🍓1
#геом_разминка #easy #9
Задача. Дан равносторонний треугольник 𝐴𝐵𝐶 с центром описанной окружности 𝑂. Пусть 𝐷 — точка на меньшей дуге 𝐵𝐶 описанной окружности, такая, что 𝐷𝐵 > 𝐷𝐶. Серединный перпендикуляр к 𝑂𝐷 пересекает описанную окружность в точках 𝐸, 𝐹, причём 𝐸 лежит на меньшей дуге 𝐵𝐶. Прямые 𝐵𝐸 и 𝐶𝐹 пересекаются в точке 𝑃. Докажите, что 𝑃𝐷 ⊥ 𝐵𝐶.
Задача. Дан равносторонний треугольник 𝐴𝐵𝐶 с центром описанной окружности 𝑂. Пусть 𝐷 — точка на меньшей дуге 𝐵𝐶 описанной окружности, такая, что 𝐷𝐵 > 𝐷𝐶. Серединный перпендикуляр к 𝑂𝐷 пересекает описанную окружность в точках 𝐸, 𝐹, причём 𝐸 лежит на меньшей дуге 𝐵𝐶. Прямые 𝐵𝐸 и 𝐶𝐹 пересекаются в точке 𝑃. Докажите, что 𝑃𝐷 ⊥ 𝐵𝐶.
❤5❤🔥3🔥3👍1👎1
#геом_разминка #hard #9
Задача. Касательные, проведенные из точки 𝑃 к окружности с центром 𝑂, касаются окружности в точках 𝐴 и 𝐵. Точка 𝐶 лежит на меньшей дуге 𝐴𝐵. Перпендикуляр к прямой 𝑃𝐶, восставленный в точке 𝐶, пересекает биссектрисы утлов 𝐴𝑂𝐶 и 𝐵𝑂𝐶 в точках 𝐷 и 𝐸. Докажите, что 𝐶𝐷 = 𝐶𝐸.
Задача. Касательные, проведенные из точки 𝑃 к окружности с центром 𝑂, касаются окружности в точках 𝐴 и 𝐵. Точка 𝐶 лежит на меньшей дуге 𝐴𝐵. Перпендикуляр к прямой 𝑃𝐶, восставленный в точке 𝐶, пересекает биссектрисы утлов 𝐴𝑂𝐶 и 𝐵𝑂𝐶 в точках 𝐷 и 𝐸. Докажите, что 𝐶𝐷 = 𝐶𝐸.
❤6👍3🔥3
#разминка #medium #7
Задача. Натуральное число 𝑁 имеет больше 400 натуральных делителей (включая 1 и 𝑁 ). Все эти делители записали на доске. Ваня стёр сто наибольших и сто наименьших из них. Среди оставшихся делителей оказалось поровну четных и нечетных. Докажите, что если бы вместо этого он стёр двести наибольших и двести наименьших делителей, среди оставшихся тоже оказалось бы поровну четных и нечетных.
Задача. Натуральное число 𝑁 имеет больше 400 натуральных делителей (включая 1 и 𝑁 ). Все эти делители записали на доске. Ваня стёр сто наибольших и сто наименьших из них. Среди оставшихся делителей оказалось поровну четных и нечетных. Докажите, что если бы вместо этого он стёр двести наибольших и двести наименьших делителей, среди оставшихся тоже оказалось бы поровну четных и нечетных.
😁22❤7❤🔥3🤣2
Сегодня на Летней школе руководителей математических кружков прошло занятие от одного из авторов нашего канала 🔥
Преподаватели учились конструировать однополостные гиперболоиды🦄 своими руками ✋, также узнали про применение поверхностей второго порядка в реальной жизни и в планиметрии
Занятие идеально подходит для школьников и взрослых всех возрастов 👶👱♂️👨🦰👨🦳
Приглашаем и вас собрать свой первый гиперболоид :)
Смотрите презентацию ниже и ищите там ингредиенты 🥒 🍅 для сборки👇
Почему предметы со слайдов имеют форму поверхностей второго порядка? Какая геометрия 📐 за этим стоит? Пишите ваши версии в комментах
Преподаватели учились конструировать однополостные гиперболоиды
Занятие идеально подходит для школьников и взрослых всех возрастов 👶👱♂️👨🦰👨🦳
Приглашаем и вас собрать свой первый гиперболоид :)
Смотрите презентацию ниже и ищите там ингредиенты 🥒 🍅 для сборки👇
Почему предметы со слайдов имеют форму поверхностей второго порядка? Какая геометрия 📐 за этим стоит? Пишите ваши версии в комментах
Please open Telegram to view this post
VIEW IN TELEGRAM
Please open Telegram to view this post
VIEW IN TELEGRAM
❤10🥰4❤🔥2
#геом_разминка #easy #7
Задача. В прямоугольном треугольнике 𝐴𝐵𝐶 с прямым углом 𝐴 вписанная окружность касается сторон 𝐴𝐵 и 𝐵𝐶 точках 𝑃 и 𝑄 соответственно. Прямая 𝑃𝑄 пересекает продолжение стороны 𝐴𝐶 в точке 𝑅. Докажите, что 𝐵𝑄 = 𝐴𝑅.
Задача. В прямоугольном треугольнике 𝐴𝐵𝐶 с прямым углом 𝐴 вписанная окружность касается сторон 𝐴𝐵 и 𝐵𝐶 точках 𝑃 и 𝑄 соответственно. Прямая 𝑃𝑄 пересекает продолжение стороны 𝐴𝐶 в точке 𝑅. Докажите, что 𝐵𝑄 = 𝐴𝑅.
❤9❤🔥4👍3
#геом_разминка #hard #10
Задача. Пусть 𝑂 — центр описанной окружности остроугольного треугольника 𝐴𝐵𝐶, а 𝐻 — его ортоцентр. Лучи 𝐴𝑂, 𝐶𝑂 пересекают стороны 𝐵𝐶, 𝐵𝐴 в точках 𝐴₁, 𝐶₁ соответственно. Точка 𝐾 — проекция 𝑂 на отрезок 𝐴₁𝐶₁, точка 𝑀 — середина 𝐴𝐶. Докажите, что ∠𝐻𝑀𝐴 = ∠𝐵𝐾𝐶₁.
Задача. Пусть 𝑂 — центр описанной окружности остроугольного треугольника 𝐴𝐵𝐶, а 𝐻 — его ортоцентр. Лучи 𝐴𝑂, 𝐶𝑂 пересекают стороны 𝐵𝐶, 𝐵𝐴 в точках 𝐴₁, 𝐶₁ соответственно. Точка 𝐾 — проекция 𝑂 на отрезок 𝐴₁𝐶₁, точка 𝑀 — середина 𝐴𝐶. Докажите, что ∠𝐻𝑀𝐴 = ∠𝐵𝐾𝐶₁.
❤10🔥4❤🔥3👍1
#геом_разминка #medium #9
Задача. В треугольнике 𝐴𝐵𝐶 точки 𝐷 и 𝐸 являются серединами сторон 𝐴𝐵 и 𝐴𝐶 соответственно. Прямые 𝐵𝐸 и 𝐶𝐷 пересекаются в точке 𝐺. Описанная окружность треугольника 𝐴𝐵𝐸 и описанная окружность треугольника 𝐴𝐶𝐷 пересекаются в точке 𝑃 (точка 𝑃 не совпадает с точкой 𝐴). Продолжение прямой 𝐴𝐺 пересекает описанную окружность треугольника 𝐴𝐶𝐷 в точке 𝐿 (точка 𝐿 не совпадает с точкой 𝑆). Докажите, что прямая 𝑃𝐿 ‖ 𝐶𝐷.
Задача. В треугольнике 𝐴𝐵𝐶 точки 𝐷 и 𝐸 являются серединами сторон 𝐴𝐵 и 𝐴𝐶 соответственно. Прямые 𝐵𝐸 и 𝐶𝐷 пересекаются в точке 𝐺. Описанная окружность треугольника 𝐴𝐵𝐸 и описанная окружность треугольника 𝐴𝐶𝐷 пересекаются в точке 𝑃 (точка 𝑃 не совпадает с точкой 𝐴). Продолжение прямой 𝐴𝐺 пересекает описанную окружность треугольника 𝐴𝐶𝐷 в точке 𝐿 (точка 𝐿 не совпадает с точкой 𝑆). Докажите, что прямая 𝑃𝐿 ‖ 𝐶𝐷.
❤5❤🔥4
#геом_разминка #medium #9
Задача. Известно, что две окружности 𝜔₁ и 𝜔₂ с неравными радиусами расположены так, что к ним можно провести общие внутренние касательные. Общая внутренняя касательная 𝑙 к 𝜔₁, 𝜔₂ и две внешние общие касательные 𝑙₁ и 𝑙₂ пересекаются в точках 𝐵 и 𝐶 соответственно. Окружность 𝛾₁, проходящая через 𝐵, касается внешним образом 𝜔₁ и 𝜔₂. Пусть 𝑃 — вторая точка пересечения 𝛾₁ и 𝑙₁. Окружность 𝛾₂, проходящая через 𝐶, касается внешним образом 𝜔₁ и 𝜔₂. Пусть 𝑄 — вторая точка пересечения 𝛾₂ и 𝑙₂. Докажите, что точки 𝐵, 𝑃, 𝐶, 𝑄 лежат на одной окружности.
Задача. Известно, что две окружности 𝜔₁ и 𝜔₂ с неравными радиусами расположены так, что к ним можно провести общие внутренние касательные. Общая внутренняя касательная 𝑙 к 𝜔₁, 𝜔₂ и две внешние общие касательные 𝑙₁ и 𝑙₂ пересекаются в точках 𝐵 и 𝐶 соответственно. Окружность 𝛾₁, проходящая через 𝐵, касается внешним образом 𝜔₁ и 𝜔₂. Пусть 𝑃 — вторая точка пересечения 𝛾₁ и 𝑙₁. Окружность 𝛾₂, проходящая через 𝐶, касается внешним образом 𝜔₁ и 𝜔₂. Пусть 𝑄 — вторая точка пересечения 𝛾₂ и 𝑙₂. Докажите, что точки 𝐵, 𝑃, 𝐶, 𝑄 лежат на одной окружности.
❤🔥4❤3🔥3👍1
#геом_разминка #medium #8
Задача. Из вершины 𝐵 прямоугольного треугольника 𝐴𝐵𝐶 с прямым углом 𝐴 вылетел бильярдный шар 🎱, который попал в середину 𝐴𝐶, потом — в точку на гипотенузе, а затем — в вершину 𝐴. Найти углы треугольника.
Задача. Из вершины 𝐵 прямоугольного треугольника 𝐴𝐵𝐶 с прямым углом 𝐴 вылетел бильярдный шар 🎱, который попал в середину 𝐴𝐶, потом — в точку на гипотенузе, а затем — в вершину 𝐴. Найти углы треугольника.
❤14🔥3❤🔥2👎2